Curiosidades matemáticas
La serie de Fibonacci
La serie de Fibonacci es una secuencia de números que empieza con dos unidades, y que prosigue sumando los dos números anteriores.
1,1,2,3,5,8,13,21,34,55,89,…
1+1=2
1+2=3
2+3=5
…
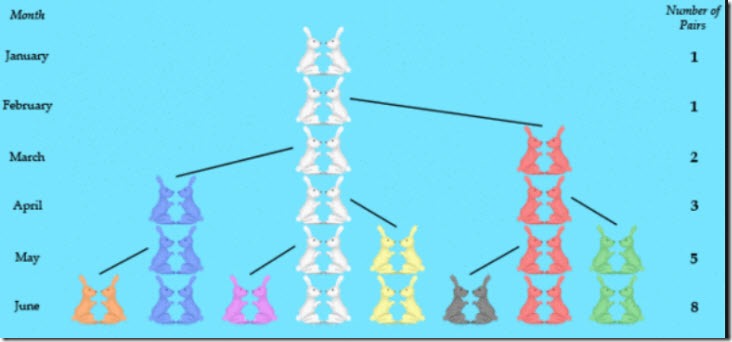
Esta serie fue definida por el matemático italiano Leonardo Pisano en 1202, conocido como Fibonacci, porque su padre se llamaba Bonacci (Fi- Bonacci = hijo de Bonacci). Esta seré obedecía a una representación matemática del número de parejas de conejo que se pueden criar, asumiendo que las conejas dan a luz siempre parejas compuestas por un macho y una hembra. Realmente esto no es así, ya que el conejo tiene camadas más numerosas, y no cada mes, pero imaginemos que es cierto.
En Enero tenemos una única pareja de conejos que dan a luz en febrero a otra pareja. En febrero, la pareja original volverá a tener descendencia, y sus crías también podrán tener. Si se sigue esta secuencia, se obtiene la serie de Fibonacci.
Esta serie puede observase en la naturaleza en ocasiones. Por ejemplo en el número de padres de una abeja macho. Los zánganos (1) provienen de huevos no fertilizados de la abeja reina, por lo que tienen solo un padre (1,1). La reina sin embargo, sí que tiene padre y madre (1,1,2). En la generación anterior, la madre de la reina era otra reina (con dos padres), y un zángano, con un solo padre (en total 3 abuelos) (1,1,2,3). Y la serie continúa así, siguiendo la secuencia de Fibonacci.
El número áureo
Al numero áureo se le representa con la letra griega phi (φ), y tiene un valor aproximado de 1,618. El rectángulo áureo es aquel compuesto por cuadrados cuyo lado sigue una progresión obtenida al dividir la longitud de sus lados por el número φ. Siguiendo con esta secuencia se pueden conseguir efectos visuales sorprendentes.
Notad que si dividimos los números de la serie de Fibonacci por su antecesor se obtiene un número cercano a φ.
89:55=1,618
55:34=1,618
34:21=1,619
21:13=1,615
13:8=1,625
Puede encontrase el número áureo en la naturaleza, y también en el arte, aunque en este caso no se puede precisar si por simple accidente o por intención del artista. En algunos libros se afirma que si se dibuja un rectángulo alrededor de la cara de la Mona Lisa , la relación de la altura y el ancho de ese rectángulo es igual al número áureo. No existe documentación que corrobore que Leonardo utilizó conscientemente el número φ, aunque es cierto que el artista era amigo personal de Luca Pacioli, que publicó un tratado en tres volúmenes sobre la Proporción Áurea en 1509 (titulado La Divina Proporción ).
Los números perfectos
Seguramente conoces a los números primos, que son los números naturales que solo son divisibles por 1 y por si mismos. Pero hay otra clasificación de números todavía más selecta. Son los números perfectos, que son aquellos cuya suma de sus factores (exceptuando él mismo) suman el valor de ese número.
Son números perfectos:
6=1+2+3
28 = 1 + 2 + 4 + 7 + 14
496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248
8128 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 127 + 254 + 508 + 1016 + 2032 + 4064
Terna pitagórica
Son conjuntos de tres números naturales que cumplen el teorema de Pitágoras: a² + b² = c²
Alguna de estar ternas son:
( 3 , 4 , 5 )
( 5, 12, 13)
( 7, 24, 25)
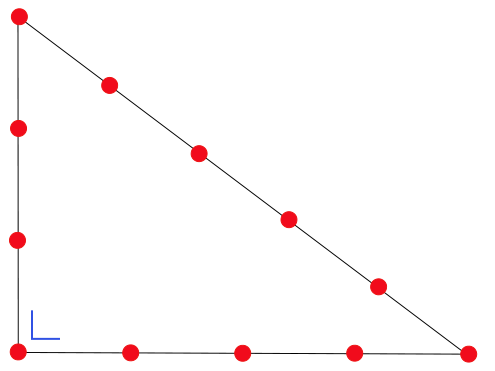
Estas ternas, que a principio pueden parecer algo banal, ofrecen posibilidades impresionantes. Por ejemplo el triángulo cuyos lados son 3, 4 y 5 unidades, era conocido por los egipcios, que lo llamaban ·el triángulo sagrado”, y lo utilizaban en sus construcciones para crear ángulos rectos.
Teorema de Fermat
La expresión an + bn = cn se cumple con números a,b y c naturales, como hemos visto, pero Pierre de Fermat conjeturó en 1637 que con potencias mayores que 2, es imposible que a,b y c sean naturales. Aunque parezca muy sencillo, este teorema no pudo ser demostrado hasta 1995, cuando Andrew Wiles presentó un artículo de ¡98 páginas! con la explicación matemática.
Números poligonales
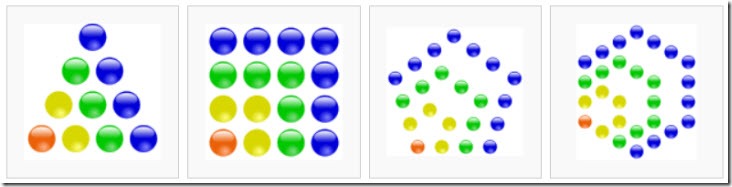
Seguro que en alguna ocasión os habéis entretenido dibujando bolitas, colocándolas componiendo formas geométricas. Los números naturales necesarios para dibujar esas formas se llaman números poligonales.
Así, los números 1,3,6,10… son números triangulares. 1, 4, 9, 16 son números cuadrados, etc.
El hotel de Hilbert
Si alguna vez os habéis alojado en un hotel y os ha parecido grande, es porque no conocéis el hotel de Hilbert. Es un hotel que tiene infinitas habitaciones. Obviamente, es un hotel imaginario, utilizado por el matemático alemán David Hilbert para explicar varias paradojas postuladas por Georg Cantor, en relación con el concepto matemático de infinito.
Dos grandes hoteleros querían hacer el hotel más grande del mundo, pero para asegurarse de que nadie construyese un hotel más grande que el suyo tendrían que hacerlo con infinitas habitaciones. El hotel fue construido e inaugurado, y pronto se llenó de infinitos huéspedes. Pero aun así había más gente que quería entrar en el hotel. Al recepcionista se le ocurrió la idea de pedir a los huéspedes que cogiesen su equipaje y se mudasen a la habitación resultado de multiplicar su número de habitación actual x2. Así todos se mudaron a una habitación par y quedaron libres todas las infinitas habitaciones con número impar. (Paradoja de infinito x2)
Georg Cantor de tanto darle vueltas al infinito y sus paradojas acabó en un psiquiátrico, así que no os obsesionéis con el concepto, no sea que se os vaya a ir la cabeza como a él.
La cuadratura del círculo
La cuadratura del círculo es un problema matemático irresoluble, consistente en hallar con regla y compás un cuadrado que tenga el mismo área que un círculo. De hecho, la expresión “esto es la cuadratura del círculo” se utiliza ante algo que no se puede resolver.
El problema se trató de resolver desde la antigüedad. Incluso los egipcios tenían mecanismos para aproximarse a la cuadratura del círculo, como se muestra en los problemas del papiro matemático de Rhind. Os aconsejo la lectura de esta otra entrada en este mismo blog que lo explica.



Nicolás
29/03/15 03:44
Lo del hotel de Hilbert invariablemente me saca una sonrisa. Es simplemente genial.
Sobre la sucesión de Fibonacci y la razón áurea por otro lado, es interesante ver que todo se vuelve muy claro si se mira por el lado correcto. Por si hay alguien que no lo sepa todavía:
La sucesión está definida de forma recurrente: a_{n+1}=a_n+a_{n-1}. Lo que quiere decir que cualquier término de la sucesión se puede escribir conociendo los 2 primeros y la relación de recurrencia que acabo de escribir. Mejor todavía, agregando a esa relación la ecuación trivial a_n=a_n, se puede escribir en forma matricial:(a_{n+1},a_n)^T=M^n(a_1,a_0)^T (la T es simple trasposición), donde la matriz M tiene entradas m_{11}=1, m_{12}=1, m_{21}=1, m_{22}=0.
Para resolver entonces todo lo que hay que hacer es diagonalizar M. La ecuación característica es precisamente phi^2-phi-1=0 que aparece al resolver a+b/a=a/b, y que tiene como soluciones L_+=(1+sqrt{5})/2 y L_-=(1-sqrt{5})/2, de los que la primera es la razón áurea. El caso particular de la sucesión de Fibonacci es a_0=0 y a_1=1, lo que deja como solución (después de algunos cálculos) a_n=(L_+^n – L_-^n)/sqrt{5}. Como L_- es menor que 1, para n>>1 se vuelve despreciable y a_n es aproximadamente igual a L_+^n/sqrt{5}. En el límite de n yendo a infinito resulta entonces a_{n+1}/a_n=L_+, como es sabido.
Lo interesante de todo esto es lo que se deduce de la solución: La razón áurea y la relación de recurrencia de la sucesión son una y la misma cosa, vista desde diferentes «coordenadas».
baneeustesss
29/03/15 09:56
¿que hay de misterioso en Fibonacci?, para un «escéptico»….
lamentira
29/03/15 10:27
@ baneeustesss:
Absolutamente nada. ¿No te gustó la entrada?
Someone
29/03/15 12:23
Curiosidades matemáticas hay en cantidad. Por añadir una, los «números de Munchausen», aquellos que son iguales a la suma de sus cifras elevadas a si mismas. Solo existen dos números de este tipo: 1=1^1 y 3435=3^3+4^4+3^3+5^5.
@ Nicolás:
Yo siempre he sido más de la cuadratura del círculo. Y idea detrás de la demostración no es demasiado complicada: básicamente con rectas y circunferencias se pueden resolver, como mucho, ecuaciones de segundo grado (ax^2+bx+c=0), y por lo tanto solo podremos construir números racionales, raíces cuadradas, raíces de grado cuatro… Y, puesto que pi es un número trascendente (lo cual sí es complicado de demostrar), no se puede construir el número pi.
Además, esta demostración también sirve con los otros dos problemas clásicos: «duplicar el cubo» (dada la arista de un cubo, construir la arista de un cubo que tenga el doble del volumen) y «trisecar el ángulo» (dado un ángulo, dividirlo en tres ángulos iguales). Ambos por la misma razón: para construirlos hay que calcular la raíz cúbica de algún número, y las raíces cúbicas no se pueden construir por la misma razón que antes.
Lampuzo
29/03/15 12:54
@ baneeustesss:
A ver.., repita conmigo…: «Cuuurioosidaaades Maaatemáááticas..»
Acaba de reafirmar nuestro conocimiento que no distingue Ud. un escéptico de una botella de Coca-Cola de dos litros..
E.T
29/03/15 14:13
1= Punto.
2= Linea.
3= Triangulo.
4= Cuadrado.
5= Pentagono
6= Hexagono.
Todo es Geometria, todo son Numeros. El Universo es una ecuacion, todo lo demas es Ilusion.
Javi
29/03/15 17:21
@ E.T:
0=Tu inteligencia.
Amildao
29/03/15 17:23
@ baneeustesss:
De diez cosas te has equivocado en once.
Tru
29/03/15 17:41
Chiste matemático
Nicolás dijo:
CarlosR
29/03/15 17:42
baneeustesss dijo:
Nada. Al contrario, es muy atractivo para los conspiranoicos junto con el número áureo, y les adjudican un carácter mágico. El problema es que no saben explicar el porqué.
CarlosR
29/03/15 17:48
Creo que viniendo de Leonardo Da Vinci nada puede ser casualidad, eso a riesgo de pasar por magufo.
Muy buena la entrada. En una época me encantaba la matemática. Me hizo acordar mis tiempos de estudiante.
Nicolás
29/03/15 21:12
@ Someone:
También es muy interesante la cuadratura. En algún momento se me ocurrió que la imposibilidad podría reducirse a la imposibilidad de encontrar una forma suficientemente «decente» de mapear el círculo en un cuadrado, donde por «decente» debe entenderse que verifica determinadas condiciones (obviamente relacionadas al método de construcción). Pero finalmente lo dejé de lado
@ Tru:
elojoktodolove
29/03/15 21:53
@ CarlosR:
..para eso te tienen a ti, ya que pareces el único listo en el foro.
…y no olvides la fotografia….
Persona
29/03/15 22:44
Sobre el cálculo de ángulos, bisectriz y trisectriz, como dibujante no me había parado a pensar en las aplicaciones practicas más allá de la representación gráfica. De ahí que confíe más en el compás que en la calculadora y el transportador (y el hecho de que la rotación del brazo de mi mesa de dibujo esté dividida en tercios de angulo recto ayuda también, no voy a mentir).
Quería simplemente compartir la anécdota.
Sun salud¤.
1984
31/03/15 18:15
Buenas tardes. Es la primera vez que leo LA MENTIRA ESTÁ AHÍ FUERA y me parece interesante. He estado buscando algún artículo que trate el Holocausto, pero no he encontrado nada. ¿Tenéis pensado tocar el tema en el futuro? Gracias
La verdad se corrompe tanto con la mentira como con el silencio.
Cicerón
zule
1/04/15 22:11
Buena entrada! me gusta mucho este tipo de posts 🙂
Tru
3/04/15 18:48
1984 dijo:
El silencio entorno al holocausto y a cualquier cosa puede que corrompa el recuerdo de lo que pasó, aunque quien sabe, también la maledicencia lo hace, ¿en qué deposita más confianza?: ¿el trabajo arqueológico, historiográfico, futuro, o el boca a boca a través de los siglos?. Quien sabe; así planteado nos olvidamos de lo ya visto y su conservación, el recuerdo citado; lo dicho hasta el mometo es tremendamente exhaustivo y no hay mentira en los hechos. En cualquier caso se puede tratar como la mentira fué utilizada por la cúpula nazi para hacer lo que hicieron.
El holocausto era un secreto a voces; se inculcó el odio a los judíos y se utilizó como arma política que luego tuvo, y hubo, de ser sustanciada,(el botín que podrían repartirse los perpetradores en pro de su causa y la mano de obra esclava también ayuda). El holocausto se hizo con mentiras, fué cosa de utilizar a la masa, la encubridora de las mismas; este es el peor silencio, el que encubre las mentiras. Ahora es cosa, en efecto, de recordar y aprhender de ese recuerdo. Cuando llegue alguien y le diga que los musulmanes son muy malos, recuerde que la masa busca enemigos para unirse…(y no hablo de Bruce Banner y Los Vengadores)…
CarlosR
3/04/15 19:11
Tru dijo:
Un «trabajo» de siglos que aún continúa. Lamentable.
Tru
3/04/15 19:52
@ CarlosR:
Si. Pero estamos montando un off-topic…como 1984 era la primera vez que posteaba cabría recomendar que tratase allí el tema…o lo sugiriese en el foro.
CarlosR
3/04/15 21:58
@ Tru:

CarlosR
3/04/15 22:00
elojoktodolove dijo:
No olvides tus vacunas bien llenitas de mercurio. 🙂
Kamu Syldeck
8/09/17 05:27
Hola:
Eso de la cuadratura del círculo, la trisección del ángulo,(este último a partir de un ángulo cualquiera), entre otras, tuvo que demostrarse que eran irresolubles, luego no son problemas. Esto significó un gran avance en las matemáticas, ya que los que se especializan en ella no tuvieron más excusas para no dedicarse a otras cosas dentro de esta ciencia formal que si podían ser productivas.
Saludos.
Luis Castano
9/09/17 02:09
Buenas noches:
He llegado a esta entrada por casualidad, al leer el comentario anterior de Kamu Syldeck. Y ya que estoy aquí quería comentar algunos puntos. No sobre la entrada en general sino sobre uno de los apartados de la misma: el dedicado al número áureo.
En ese apartado se dice:
«Puede encontrarse el número áureo en la naturaleza (link), y también en el arte, aunque en este caso no se puede precisar si por simple accidente o por intención del artista. En algunos libros se afirma que si se dibuja un rectángulo alrededor de la cara de la Mona Lisa , la relación de la altura y el ancho de ese rectángulo es igual al número áureo. No existe documentación que corrobore que Leonardo utilizó conscientemente el número φ, aunque es cierto que el artista era amigo personal de Luca Pacioli, que publicó un tratado en tres volúmenes sobre la Proporción Áurea en 1509 (titulado La Divina Proporción).»
Bien, pues con permiso del autor de la entrada me gustaría señalar algunas dudas o incorrecciones ya que conviene no confundir el número áureo (1’618) y su trazado geométrico con la Divina Proporción. Me explico.
Ciertamente, Leonardo ilustró el libro de Luca Pacioli y en algunas de las figuras aparece, por construcción, la proporción áurea. Es el caso, por ejemplo, del pentágono regular.
Sin embargo, parece ser que cuando Pacioli habla de la Divina Proporción no se refiere a la proporción áurea sino al Canon y al Sistema de Medidas Antiguo, que llega hasta su época a través de Vitruvio. Esto es al menos lo que señalan distintos autores:
http://terraeantiqvae.com/profiles/blogs/el-famoso-numero-aureo-podria-no-ser-mas-que-un-prolongado-engano
En mi caso particular comparto esa opinión ya que, tras estudiar el documento en el que Leonardo recoge el Canon, he podido confirmar que, en contra de lo que suele decirse, la relación altura / ombligo en el Hombre en T no cumple la proporción áurea (1’618) sino que estamos ante una relación en Dedos (100 Dedos / 61 Dedos = 1’639).
Por otro lado en las notas del documento Leonardo no habla en ningún momento del trazado geométrico de la proporción áurea sino de la cuadrícula de medidas antropométrica, medidas que recoge en la línea horizontal a los pies del cuadrado.
En cuanto a que el número áureo se encuentre en la naturaleza y en el arte es un tema que aún está en discusión. En la web del link facilitado en la entrada se señala que:
«Algunos autores sugieren que el número áureo se encuentra como proporción en varias estelas de Babilonia y Asiria de alrededor de 2000 a. C. Sin embargo, no existe documentación histórica que indique que el número áureo fuera utilizado conscientemente por dichos artistas en la elaboración de las estelas. Cuando se mide una estructura compleja, es fácil obtener resultados curiosos si se tienen muchas medidas disponibles. Además, para que se pueda afirmar que el número áureo está presente, las medidas deben tomarse desde puntos significativos del objeto, pero este no es el caso de muchas hipótesis que defienden la presencia del número áureo. Por todas estas razones Mario Livio concluye que es muy improbable que los babilonios hayan descubierto el número áureo.»
Efectivamente, lo que parece encontrarse en muchos edificios de la Antigüedad no es (como se dice) la proporción áurea sino la cuadrícula del Sistema de Medidas Antiguo.
Con respecto a la naturaleza pues aún no está claro. Si no recuerdo mal, autores como Georges Markowsky (en su trabajo Misconceptions about the Golden Ratio) defienden que no pero sus objeciones han sido a su vez criticadas por otros estudiosos.
Señalar por último que la moda de ver a la Proporción Áurea por todas partes (y como criterio ¿objetivo? de belleza) parece haber comenzado con los trabajos de Matila Ghyka, que luego influyeron en Le Corbusier y en Dalí. Estos autores sí emplearon conscientemente la proporción áurea en (algunas de) sus obras. Pero de ahí a verla por todas partes (sin justificación suficiente) va un abismo. En este sentido, para quien le guste como a mí la composición en pintura, recomiendo el libro «Tramas. La geometría secreta de los pintores» de Charles Bouleau.
Con esto no pretendo, ni mucho menos, criticar la entrada de más arriba (que me parece muy interesante) sino aportar algo más a la misma con respecto a la tan traída y llevada Proporción Áurea.
Un cordial saludo. Luis Castaño. Licenciado en Filología. Investigador en Metrología.