Con π de pirámide
Hoy en día todavía hay mucha gente que cree que las pirámides fueron construidas por extraterrestres o atlantes. Los primeros cristianos y musulmanes creían que fue el propio Dios el que las creó. No hemos cambiado mucho en estos últimos siglos. Solo hemos remplazado una túnica por un traje espacial.
Un interesante argumento que apunta a que fue una inteligencia super avanzada la que diseñó las pirámides de la 4ª dinastía en Giza, es la presencia insolente del número [latex]\pi[/latex] en sus dimensiones, cuando según los egiptólogos, los egipcios no conocían los números reales, y solo se manejaban con fracciones de números enteros.
Recordemos que el número [latex]\pi[/latex] es el resultado de dividir el perímetro de una circunferencia entre su diámetro, y su valor es 3,1416.
¿Dónde aparece el número [latex]\pi[/latex] en las pirámides?
Los lados de la gran pirámide de Giza tienen las siguientes longitudes
- Lado Oeste: 230,357 m
- Lado Norte: 230,253 m
- Lado Este: 230,391 m
- Lado Sur: 230,454 m
Por lo tanto, el perímetro de la pirámide es:
P = 230,357 + 230,253 + 230,391 + 230,454 = 921,455 m
La altura de la pirámide es 146,5 m.
Si el perímetro de una circunferencia es:
P = 2 · [latex]\pi[/latex] · r
donde r es el radio, entonces
$latex \pi = { P \over 2 * r}$
Sustituyendo P por el perimetro de la pirámide y r por la altura obtenemos:
$latex \pi = {921,455 \over 2* 146,5} = 3,1449$
Una buena aproximación al número $latex \pi$, con un error de solo 3 milésimas. ¿Casualidad?
El papiro matemático de Rhind
Este papiro data del 1800 a.C. aproximadamente y contiene el enunciado y resolución de 87 problemas matemáticos, por lo que es un elemento valiosísimo para entender el nivel de conocimiento que tenían los egipcios en la época de las pirámides. En este papiro hay varios problemas interesantes, pero fijémonos ahora en el número 50. El enunciado del problema plantea cómo calcular el área de un círculo que tiene 9 unidades de diámetro (digamos metros). Para resolverlo se explica que hay que quitar 1/9 del diámetro y al resultado multiplicarlo por si mismo. El resultado es el mismo que el área del circulo.
Los egipcios tenían una curiosa manera de multiplicar. Por ejemplo para calcular el valor de 8 * 9, tomaban una de las dos cifras a multiplicar y hacían una tabla como la siguiente, en la que se duplicaba el valor en cada iteración
1…8 «
2…16
4…32
8…64 «
Como se quiere multiplicar por 9, tomamos los valores asociados al 8 y al 1 y los sumamos: 72 (que es 8×9)
En el problema que nos atañe, es incluso más fácil, ya que hay que tomar el valor asociado al 8: 64 $latex m^2$(8×8). El valor real de la superficie de la circunferencia es:
A = $latex \pi$ · $latex r^2$ = 63,6173 $latex m^2$
El resultado es bastante aproximado. Pero lo más inquietante es que en base a este método de cálculo se podría inferir un valor aproximado a $latex \pi$ expresado como fracción de números enteros:
a: área
d: diámetro
r: radio (2*r)=d
$latex a = (d-{d\over 9})^2$
$latex a= (d * (1- {1 \over 9}))^2$
$latex a= (d * {8 \over 9})^2$
$latex a= d^2 * {64 \over 81}$
$latex a= (2 * r)^2 * {64 \over 81}$
$latex a= 4 * r^2 * {64 \over 81}$
$latex a= r^2 * {256 \over 81}$
Según esta aproximación, los egipcios estaban aproximando a $latex \pi$ con la fracción $latex {256 \over 81}$ = 3,1605. ¿Otra coincidencia? Posiblemente si. Lo más seguro es que los egipcios empíricamente se hubiesen dado cuenta de que la aproximación detallada en el problema 50 del papiro de Rhind era lo suficientemente buena para darla por válida.
Si realmente hubiesen descubierto este factor constante en todas las circunferencias, no lo manejarían como $latex {256 \over 81}$, sino como fracciones de numerador igual a la unidad:
$latex {256 \over 81}$ = 3 + $latex {1 \over 9}$ + $latex {1 \over 27}$ + $latex {1 \over 81}$
Pero estas fracciones son muy incómodas de manejar en el sistema egipcio de multiplicación, pues todos los denominadores son impares, y ellos siempre trataban de evitarlos.
Explicaciones
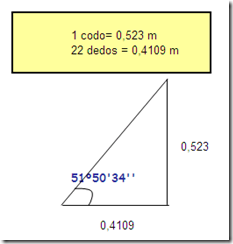
Una explicación sencilla a la presencia de $latex \pi$ en las proporciones de la gran pirámide es la manera en la que se construían. Por ejemplo, en los problemas 56 a 60 del papiro matemático de Rhind se enseña a calcular la pendiente de las paredes de una pirámide, lo que ellos conocían como seked. Para los egipcios el seked era la distancia en el plano horizontal que se desplaza la pared de la pirámide por cada codo que se levanta en altura. Un codo equivale aproximadamente a 0,523 metros. Un codo = 7 palmos y un palmo=4 dedos.
La pirámide de Keops tiene un seked de 22 dedos, o bien de 5½ palmos. Eso quiere decir que por cada codo que se eleva, pierde 5 palmos y medio en el plano horizontal.
Debido a la relación entre dedos y codo de 1 a 28, los egipcios podían construir con 28 sekeds distintos, desde 1, casi vertical, a 28 (45 grados). Todas las pirámides de Egipto están construidas con uno de estos sekeds, pero los mas comunes eran el 22, el 21, 19, 23 y 24. Hay alguna excepción que tiene un seked de más de 28 dedos, como la de Sneferu (30), con una inclinación algo menor de los 45º.
Los egipcios construían las pirámides desde fuera hacia dentro. Primero colocaban las piedras exteriores que eran cortadas con el seked de la pirámide, y luego se rellenaba el interior. Al llevar implícito este ángulo de inclinación de 51º 50’ 34”, por mera coincidencia se cumple lo expuesto en la primera parte de este artículo, al igual que ocurre en las pirámides de Huni y de Niuserra, y no ocurre por ejemplo en la de Micerinos, que tiene un seked de 23.
Hay otra teoría que a mi me gusta más (aunque no quiera decir que sea más plausible). Al medir la longitud de los lados de la pirámide normalmente habrían usado una cuerda, pero en distancias tan grandes como 230 metros, hasta las cuerdas más sólidas tienen cierta elasticidad. Es posible que en vez de utilizar una cuerda utilizasen una rueda para medir la longitud, con lo que se evitaría este problema. Imaginad una rueda cuyo diámetro sea un codo (0,523 m.) y por tanto su perímetro sea 1,643m. Para conseguir alcanzar los 230 metros de lado de la pirámide, debió de dar 140 giros completos. Si para calcular la altura se hubiesen estimado apilar tantos diámetros como el doble de giros dados por la rueda para dibujar el lado, entonces la altura sería 2 · 140 * 0,523m = 146,44m, exactamente la altura de la pirámide. En este caso también habría quedado grabada la impronta del número $latex \pi$ en las dimensiones de la pirámide, sin que los egipcios hubiesen tenido constancia de ello realmente.
Referencias:
http://www.3viajesaldia.com/el-misterio-de-pi-y-las-piramides-de-egipto/
http://www.egiptomania.com/jeroglificos/articulo/relaciones.htm
http://www.egiptologia.org/ciencia/matematicas/aritmetica_fracciones.htm

NewZealander
25/07/12 09:45
Anónimo dijo:
Te se nota kas hynbestygao la rehostia
http://www.institutoestudiosantiguoegipto.com/Transporte%20piedras2.htm
Filthy AnimaL
1/03/14 02:53
Es fácil «descubrir» y entender el número Pi. Toma una circunferencia y enrolla una cuerda a su alrededor. La cantidad de cuerda justa para cubrir todo el perímetro es exactamente 3.1416 veces que el diámetro de esta. Hasta un niño lo entendería.
Jiskal
9/08/14 22:48
A mí lo único que me asombra a día de hoy es la capacidad que tenían para, sin servirse de maquinaria, manejar pedrolos de hasta 60 toneladas. Qué pedazo de bestias!!
MaGaO
10/08/14 01:20
@ Jiskal:
Qué avispados, diría yo. Sin maquinaria se han movido bloques de hasta unas 1500 toneladas. Y los egipcios movieron bloques muchísimo más grandes: el coloso de Ramsés II en el Ramesseum podría haber alcanzado las 1000Tm (y encima lo desplazaron más de 270km por tierra). Y sólo es uno de los ejemplos de pedruscos enormes que han movido los egipcios.
Jiskal
10/08/14 02:21
Sí. Es lo que yo no entiendo todavía. Sin hacer uso de poleas… y aún en el caso de que hubieran hecho uso de ellas… me parece increíble que lograsen moverlas. Ya no te cuento por arrastre sobre una plataforma. Nada más que hace falta estudiar un poco de física para darte cuenta de las fuerzas que hay que vencer: gravedad, rozamiento, resistencia de material… Parece sencillo, pon 30, 50, o 100 tíos a tirar del pedrusco, pero al final si haces los cálculos te salen barbaridades como que tendrían que tirar del bloque más de 600 tíos para que cada uno se encargara de mover 100 kilos, y eso si no tenemos en cuenta la fuerza de rozamiento, que en bloques de ese tamaño viene a ser bastante importante, ni la inclinación de la rampa… Uf, pues eso, que es una pena que no dejaran planos de cómo demonios llevaron a cabo las fases de la construcción. Quién sabe, quizás hasta aprendiéramos algo nuevo incluso con la técnica que tenemos hoy en día.
MaGaO
10/08/14 11:55
Jiskal dijo:
Y sin embargo lo hicieron.
Sólo la presión: la resistencia del material depende de la distribución de presiones, el rozamiento depende de la distribución de presiones. Las rampas inclinadas requerir un poco de arrastre extra, pero los egipcios se cuidaban mucho de ajustar las rampas.
Agradecería que explicaras un poco más tus cálculos: si no tienes en cuenta el rozamiento o la inclinación de la rampa, una persona es suficiente para mover un bloque de 60Tm. Eso sí, no esperes que tenga una gran aceleración 😉
Por contra, si empezamos a considerar el rozamiento… el coeficiente de rozamiento de la madera puede ser inferior a 0.1 en circunstancias muy favorables. Pero supongamos que es 0.2 como parece ser en la mayoría de los ejemplos del enlace que he puesto: las 60Tm se convierten en 12Tm. Y ahora probablemente no necesites 600 personas para mover el bloque.
Añadamos una pendiente del 1%: una centésima del peso del bloque «tira hacia abajo», que son 600Kg. Y tienes que una masa de 60Tm requiere una fuerza de 13Tm para desplazarla con cierta holgura.
Permíteme dudarlo: como ya he dicho, sin máquinas ya se movieron bloques muchísimo más grandes. Y, hoy día se han hecho construcciones muchísimo más difíciles que las pirámides en periodos de tiempo mucho más cortos. Si bien hay que reconocerles el ingenio, me parece que en técnicas de construcción hay muy poco que aprender de ellos. Los que sí se lo curraron fueron los romanos, que desarrollaron un hormigón capaz de aguantar el agua de mar durante siglos sin romperse… pero hace relativamente poco se descubrió cómo lo hacían.
MaGaO
10/08/14 12:42
Doc Halliday dijo:
En este caso se me quedó clavado el hecho de que usaran cenizas volcánicas en la mezcla: véase más al respecto.
Jiskal
10/08/14 13:40
@ MaGaO: Lo que no entiendo aún es lo de que las 60 toneladas se convierten en 12. Podrías explicármelo más detalladamente?
Lo que no entiendo aún es lo de que las 60 toneladas se convierten en 12. Podrías explicármelo más detalladamente? 
Jaja, vale, muchas gracias por contestar. Ahora ya me queda un poco más claro el tema.
MaGaO
10/08/14 14:00
Jiskal dijo:
La fuerza de rozamiento es el producto del peso por el coeficiente de rozamiento (una constante que depende de las características propias de las superficies en rozamiento y la superficie de contacto) por el coseno del ángulo que forma la superficie de rozamiento con la horizontal.
Ignorando el detalle de que el coeficiente de rozamiento estático (cuando hay que iniciar el movimiento del objeto sobre la superficie) es superior al dinámico (cuando el objeto ya está en movimiento y hay que mantener dicho movimiento) y suponiendo que la superficie es horizontal (para que el coseno sea 1), la fuerza de rozamiento se reduce al peso del objeto por el coeficiente de rozamiento. Así, una masa de 60Tm genera un peso de 60.000 kilopondios (un kilopondio es 1kg*9,8m/s^2, el «peso» de una masa de 1kg) que, multiplicado por el coeficiente de rozamiento (0,2 según los datos típicos del enlace que puse para madera sobre diferentes superficies), resulta una fuerza de resistencia de 12.000 kilopondios. Si suponemos que una persona media es capaz de ejercer una fuerza de empuje de unos 30kilopondios (véanse unas tablas al respecto, en libras, y recuérdese que 1lb=0,454kg aproximadamente), entonces mover esas 60Tm requieren unas 400 personas. No es una cantidad pequeña, lo reconozco, pero sí asequible para un imperio como el egipcio. Más aún, hablo de la fuerza media que puede ejercer una persona: cabe esperar que los contratados para tirar de estos bloques tengan un entrenamiento (aunque sólo sea a base de tirar un día tras otro de estas cosas) que los haga capaces de empujar más que una persona media.
Nota: hablo de empujar porque las pinturas egipcias muestran a los porteadores inclinados hacia adelante, no tirando de espaldas.
Oops, se me pasó el detalle importante: cuando «convierto» las 60Tm en 12Tm es porque asimilo kilogramos de «peso» a los kilopondios que he usado en la explicación anterior. Si trabajásemos con newtons, la unidad de fuerza del SI, entonces el peso de la masa de 60Tm serían 588kN y la fuerza de resistencia sería 117,6kN. Pero pienso que es más comprensible trabajar con «toneladas» de fuerza por simplificar el asunto 🙂
obelar
16/10/14 16:28
@ Jiskal:
hombre, teniendo en cuenta la forma en que movieron los romanos los obeliscos egipcios, parece dificil de creer que los egipcios lo hicieran solo con ayuda de la fuerza bruta y tecnología rudimentaria.
Bruno,
13/01/15 08:17
Nachin58 dijo:
Esto esta fuera de tiempo, el problemas principal es no hay presupuesto. En muchas piedras están mal cortado, sólo algunas piedras muy selectas están cortada con exactitud mimilectrica, hay afueras mayorías cortada cortada algo mal.
Siempre me preguntado por que no hay arcos dentro de la pirámides. Contrulleron una camara internas sin haber piche arcos.
MaGaO
13/01/15 13:58
Bruno, dijo:
Porque desconocían la técnica necesaria para hacer arcos. Por lo que estoy leyendo, parece que lo más avanzado que llegaron a desarrollar los egipcios fue el arco adintelado, que puedes ver en esta imagen:

Hubo que esperar a las culturas mesopotámicas del segundo milenio a. de C. para que alguien lograra hacer un arco de medio punto.
Tru
13/01/15 14:50
@ MaGaO:
Así parece que fué; creo recordar que los primeros indicios arquitectónicos del uso del arco se encuentra en las bóvedas de cañón sumerias para sus alcantarillados…para atreverse a hacer arcos con piedra, pues los mencionados eran de ladrillo, hubo que pasar por las experiencias del triángulo de descarga como en la puerta de los leones en Micenas, o la arquitectura arquitrabada egipcia con arcos adintelados…
Por otro lado, podemos imaginar como el dintel es el origen del arco. Cuando una luz era lo suficientemente grande como para no ser cubierta con una sola pieza pétrea, pensaron poner dos, y luego tres…y vieron que las dovelas de los arcos adintelados aguantaban mejor, no se deslizaban tanto, si descansaban la una sobre la otra con cierta inclinación, aumentando el rozamiento entre las dovelas, piezas del arco. Esta inclinación podía conseguirse, sin cambiar la geometría prismática del dintel, cortando las piezas que lo formarían con dichas inclinaciones en las juntas, esto es, en lugar de pequeños prismas, hacía pequeñas cuñas, que viene siendo el concepto de «clave», pieza fundamental del arco…
MaGaO
13/01/15 15:35
@ Tru:
De hecho tengo que agradecer la pregunta de Bruno porque lo más que sabía yo, previo al uso de arcos de medio punto romano, era el falso arco logrado mediante dinteles superpuestos a los que se quitaba la parte central para dar la impresión de que era un arco (o los lados de un triángulo, en los modelos más toscos).
jota
16/03/15 05:01
Es facil mover cualquier cosa con esclavos si se pone todo un pais a empujar pues mueves lo q sea si se ponen hasta le dan la vuelta a tu casa jajaja
William Clavijo Robinson
25/11/15 17:41
NUEVO DESCUBRIMIENTO
Fórmulas usadas en el Diseño Arquitectónico de Keops
Pi/2 * (10 * ((7 * 4 + /(PI/7)/4^2*10))*4) = 439,999 (Base Keops codos)
(10 * ((7 * 4 + /(PI/7)/4^2*10))*4) = 280,112199737628 (Altura Keops codos)
439,999 * PI/6 = 230,38 (Base en metros)
280,112199737628 * PI/6 = 146,67 (Altura en metros)
439,999 / 280,112199737628 = 3,141592658979
O Pudieron usar esta más simple:
10 * ((2Pi * 7) /Pi/2) = 280 codos
10 * ((2Pi * 7) = 438,8229715025710
280 codos * Pi/6 = 146,607657167524
438,8229715025710 * Pi/6 = 230,290769358751
Pi = 438,8229715025710 / 280 = 3,141592658979
Las fórmulas se generan en la Cuadratura del Círculo Unitario
O simplemente esto
Pi/2 * (10 * ((7 * 4 + /(PI/7)/4^2*10))*4) = 439,999 (Base Keops codos)
10 * ((2Pi * 7) /Pi/2) = 280 codos (Altura Keops)
400 / 280 = 3,14285714285714
A pesar de partir de la cuadratura unitaria, con el conocimiento del Pi verdadero, determinan mediante una relación el valor de la base (400 codos) y con otra la Altura (280 codos), la que nos arroja una aproximación de PI de 3,14285714285714 (Pi de Arquímedes 2000 años después de Keops). Jugaban con los números.
2 es el diámetro del círculo
4 es el área del cuadrado circunscrito al círculo unitario
1 es el radio
El perímetro es = 8
El perímetro menos el radio = 7
10 es el factor de Escala
Saludos a todos
William Clavijo Robinson
1/12/15 07:00
Simplemente esto
Pi/2 * (10 * ((7 * 4 + /(PI/7)/4^2*10))*4) = 439,999 (Base Keops codos)
10 * ((2Pi * 7) /Pi/2) = 280 codos (Altura Keops)
2 es el diámetro del círculo
4 es el área del cuadrado circunscrito al círculo unitario
1 es el radio
El perímetro es = 8
El perímetro menos el radio = 7
10 es el factor de Escala
Pi en Kefrén
123 * 7 = 861m (Perímetro Kefrén)
Base: (861 m / π/6) /4 = 411,097218006366 codos (Base en codos)
Base: 411,097218006366 codos * π/6 = 215,25 metros (Base en metros)
Altura: 861 m / π = 274,064812 codos
Altura: 274,064812 codos * π/6 = 143,5 metros
Pi = 861 / 274,064812 = 3,14159265358979
Pi (π) en Mycerinus
Base Menor Pirámide = 335 pies = 102,108 metros
102,108 metros * π/2 = 65 metros (Altura Mycerinus)
Cinco Aproximaciones rápidas de Pi con 14 dígitos (Rectificación)
1. 3 +√2/10 + (√2/2 +1)/10^4 + (√3/2 +5)/10^7 + ((√√2 + 6) +7/10^3)/10^11 = 3,14159265358979
2. (7 +1/10) / ((9 + 4/100)/4) – ((8/√2) – 3) + 1/100)/10^7) – 1/(√1,25 + √0,5 + √2 + √3 + √5 + √7 + √8)*10^10 + (√3/2)/10^14 = 3,14159265358979
3. 6*((√1,25 +1,5)/5) – (2 + √8)/10^5) + (4/√7)/10^7 + 1/ (√√8 +10)*10^10
4. + 1 / (√1,25 – 4/1000)/10^10 = 3,14159265358978
5. 4*(0,5 + ((√0,5 +5)/10)/2) + ((2 + √0,5) + 1)/10 + (1 / (√7/10)) /10^4 + (√5/10 + √2)/10^6 + (2/√7)/10^10 + ((8 + √7) – 0,5)/10^12 = 3,14159265358979
6. √8 + 0,25 + 0,0625 + (1 /(150 + ((√7 + 3)/10) + 2)/10)*10) + 1 / (√0,5/3)*10^11
7. + 1 /(7 + √5) / √7)*10^12 = 3,14159265358979
Someone
1/12/15 11:26
@ William Clavijo Robinson:
Permítame ponerlo en duda.
Esto…. ¿Seguro que ha escrito la fórmula bien? Porque veo una fracción sin numerador…
Suponiendo que se le haya colado un / extra, la fórmula Pi/2*(10 *((7*4 +(PI/7)4^2*10))*4) en todo caso da 1776.92, no 439.999.
Usted ha elegido ahí Pi/6 porque aproximadamente es 0.523, el valor comúnmente aceptado del codo real egipcio (aunque se han encontrado varas de un codo dentro del rango de 0.523 y 0.529 metros). Sin embargo si tomamos más decimales tenemos que Pi/6=0.5235988, con lo que redondea a 0.524. Y al final acaba usted teniendo unos 20 o 30 cm de más.
Y, ¿no es usted lo suficientemente inteligente para ver que los factores de pi se cancelan en su «novedoso descrubrimiento» dejando solo 10*7*4?
Lo siento, no se acepta esa frase ya que usted desconoce el significado de ella y la usa solo para intentar aparentar que tiene algún conocimiento.
Ah, que ahora el «pi verdadero» es 3.4285714… Por eso cuando uno mide la longitud de una circunferencia y divide por su diámetro le sale 3.14159….
Lo siento, el perímetro del cuadrado circunscrito al círculo unitario es 4*sqrt[2], aproximadamente 5.65685…, no 8. Y en cuanto al perímetro del círculo unitario, este es (obviamente) 2*pi=6.283185… Ninguno de los dos es 8.
Lo siento, eso da 3.1415926535899306092 en lugar de lo que usted dice.
Además, ¿llama a eso aproximaciones rápidas? No sé, pero yo no le veo nada de rápido… Para eso se coge uno alguna de las series (como la de Euler 2*sum[n!/(2n+1)!!]) y casi acaba antes…
Y todo esto son errores sin entrar a criticar que toma los tamaños que le apetece para las dimensiones de las pirámides…. (Sí, cercanos a los reales, pero lo suficientemente deformados para hacer sus cábalas…)
William Clavijo Robinson
1/12/15 18:19
Respondo con datos reales y concretos tus comentarios, sin caer en la grosería o el insulto
Pi/2 * (10 * ((7 * 4 + (PI/7)/4^2*10))*4)
Efectivamente faltaba un /
DESGLOSE:
Pi/7 = 0,448798950512827
(Pi/7) / 160 = 0,00280499344070517
0,00280499344070517 * 4 = 0,0112199737628207
7*4 = 28; 28 + 0,0112199737628207 = 28,0112199737628
10 * 28,0112199737628 = 280,112199737628
280,112199737628 * Pi/2 = 28,0112199737628 * 1,5707963267949 = 439,999214438304 (Base)
No les vas a exigir al maestro constructor que te ponga los 439,999 codos porque caerías en el plano de lo ridículo, simplemente por sentido común y lógico redondeas a 440
10 * ((2Pi * 7) /Pi/2) = 280 codos (Altura Keops)
2Pi = 6,28318530717958
6,28318530717958 * 7 = 43,9822971502571
43,9822971502571 / Pi/2 = 43,9822971502571 / 1,5707963267949 = 28
10 * 28 = 280 codos (Altura Keops)
Pretender desacreditar al otro es fácil, pero por lo menos tomémonos el tiempo de investigar un poquito: Respecto al círculo Unitario (radio uno). Traza con el compás el círculo de radio 1 y circunscribe el cuadrado; si el diámetro de este círculo es 2, lógicamente su perímetro es 8: 2*4 = 8.
Respecto a las fórmulas de aproximación Pi, sabemos que existen los algoritmos para el cálculo de los infinitos decimales de Pi con varios cientos de millones; solo se trata de un Ejemplo demostrativo que se puede lograr una aproximación manual y sencilla de Pi hasta con 14 dígitos, y que también se puede lograr una aproximación a la cuadratura del círculo unitario de hasta con 8 dígitos (en AutoCAD), cosa jamás lograda por nadie y solo mediante el uso de segmentos adimensionales y círculos, sin el uso de ninguna relación, formula ni medida. Tengo unas 10 graficaciones en AUTOCAD, que respaldan lo manifestado.
Respecto a la coincidencia del Pi en Kefrén que dices:
Pi en Kefrén
123 * 7 = 861m (Perímetro Kefrén)
Base: (861 m / π/6) /4 = 411,097218006366 codos (Base en codos)
Base: 411,097218006366 codos * π/6 = 215,25 metros (Base en metros)
Altura: 861 m / π = 274,064812 codos
Altura: 274,064812 codos * π/6 = 143,5 metros
Pi = 861 / 274,064812 = 3,14159265358979
Cordiales Saludos
William Clavijo
William Clavijo Robinson
2/12/15 04:56
Otra demostración más simple de los cálculos utilizados por los egipcios en el Diseño Arquitectónico de la Pirámide de Keops
8 = Perímetro del cuadrado circunscrito al círculo unitario
Pi/2 = Base triángulo menor inscrito en cuadratura de círculo unitario
√ 8 = Diagonal del Cuadrado circunscrito al círculo unitario
Pi/2 + √ 8 = 4,39922345154109 (Base proyectada para pirámide de Keops), es decir a la base del triángulo menor (cara de pirámide) le sumaron la diagonal del cuadrado circunscrito: (√2 a cada lado).
2/(Pi/2) = 1,27323954473516 (Pendiente triangulo cuadratura circulo unitario)
4,39922345154109 / 2 = 2,19961172577054 (Mitad de Base de la figura proyectada)
2,19961172577054 * 1,27323954473516 = 2,80063263231422 (Altura proyectada para pirámide de Keops)
4,39922345154109 * 100 = 439,922345154109 codos (440) (100 = factor de escala)
2,80063263231422 * 100 = 280,063263231422 codos (280)
439,922345154109 * Pi/6 = 230,34 (Base Keops en metros)
280,063263231422 * Pi/6 = 146,64 (Altura Keops en metros)
Los reto a que cojan la cuerda, utilicen las supuestas palmas y dedos, algunos hablan de rodar una rueda (lo egipcios no conocían la rueda), pero en fin, les doy la ventaja de que se valgan de la rueda, utilicen la cuerda, las palmas y dedos y simplemente me tracen la base de la pirámide y además les doy la ventaja de que utilicen una brújula (que los egipcios desconocían) y me orienten los cuatro puntos cardinales de las distancias que medirán con la rueda, cuerda, palmas y dedos y en otro Post me comentan como les fue y que precisión lograron, ojala se acerquen siquiera un poco a la precisión lograda por los “Pobres” Egipcios.
Simplemente redondearon los valores a 440 y 280 y es lógico, si voy a construir una pared de 28 metros en mi casa, no le voy a pedir al maestro albañil que me la construya de 28 metros con 0,0063 milímetros, ya que será tomarle el pelo, pobre maestro, me dirá, vea no sea malito déjela en 28 por el favor de Dios.
Someone
2/12/15 10:17
@ William Clavijo Robinson:
¿Le tengo que recordar el orden de operaciones? (PI/7)/4^2*10=(Pi/112)*10=10*Pi/112
Por cierto, nótese que al final lo único que usted está escribiendo es (pi/2)*280+corrección del 0.04%, si luego la base la escribe simplemente como una forma complicada de escribir 280, normal que el cociente le de pi/2….
Usted sí que cae en el plano de lo ridículo: quiere sostener la hipótesis de que el número pi está representado pero lo único que hace es poner números al azar para que le cuadren las cosas y luego ignora los decimales porque «es lógico redondear».
De nuevo Pi no pinta nada en esa relación, es solo una forma complicada de escribir 10*2*7*2=280
(Bueno, en realidad de escribir 70, de nuevo debido al orden de operaciones: ((2Pi*7) /Pi/2=(2*7)/2=7. Debería haber escrito (2Pi*7) /(Pi/2) para obtener 28).
Solo porque usted lo pone demasiado fácil, cometiendo errores básicos.
Ahí admito mi fallo, estaba pensando en el cuadrado inscrito.
Llega usted tarde, aquí tiene un método para llegar hasta la precisión que uno quiera: http://www.researchgate.net/publication/280238616_approximations_in_drawing_pi_and_squaring_the_circle
Permítame dudarlo porque hasta el simple hecho de sumar (aunque sea gráficamente) es usar una relación.
Además, ¿no le han dicho ya que no se puede cuadrar el círculo con regla y compás? Todo porque Pi no es un número algebraico.
La rueda llegó a Egipto en el siglo XVI a.C., por lo que para la época de Ramsés II ya se conocía.
Entonces, si usted ya va a ponerse a aproximar desdeñando centímetros y milímetros, ¿cómo puede hablar de precisión de pi de 14 dígitos?
William Clavijo Robinson
2/12/15 14:55
Además, ¿no le han dicho ya que no se puede cuadrar el círculo con regla y compás? Todo porque Pi no es un número algebraico. Es un Hobby o entretenimiento mio, buscar una aproximación de Pi mediante una aproximación racional de La Cuadratura. No estoy descubriendo el agua tibia porque al igual que Usted, se que Pi es un numero Irracional y Trascendente. Pero es un bonito entretenimiento practicado por muchas personas que no tienen un criterio cerrado y que además te activa las neuronas.
La rueda llegó a Egipto en el siglo XVI a.C., por lo que para la época de Ramsés II ya se conocía. Pero No en el Tiempo que se construyeron las pirámide de GUIZA que es a lo que me refiero.
Usted sí que cae en el plano de lo ridículo: quiere sostener la hipótesis de que el número pi está representado pero lo único que hace es poner números al azar para que le cuadren las cosas y luego ignora los decimales porque «es lógico redondear».En la explicación de mi fórmula no redondeo ningún valor los 439,999 y más decimales es lo que arroja el cálculo, lo que manifiesto es que para cualquier constructor inclusive de la actualidad, le resultaría algo complicado manejar en una construcción una cifra como la mencionada:439,999 o 280,063263231422
Llega usted tarde, aquí tiene un método para llegar hasta la precisión que uno quiera: Es un pasatiempo, te recomendaría que lo intentes para que despejes la mente, lo que me recomiendas que vea ya lo he visto, generar un algoritmo computacional partiendo de una relación en la que para llegar a 14 dígitos tienes que haber introducido varias decenas de miles interacciones.
Entonces, si usted ya va a ponerse a aproximar desdeñando centímetros y milímetros, ¿cómo puede hablar de precisión de pi de 14 dígitos. Otra vez, Yo no estoy aproximando nada, solo manifiesto que es muy complicado para un maestro constructor manejar milímetros en una construcción, cuando su maestro albañil le construya una pared de 10 metros no creo que le vaya a comprobar si le falto o se paso con un milímetro, o no le vas a pedir que te construya una pare de 9,9999 mm o 10,001 mm, simplemente por sentido común y lógico la deja en 10 metros.
Con lo expresado en el Blog no pretendo vender ni promocionar nada, ni cambiar el criterio de Nadie, solo hago ver que hay algunas coincidencias muy cercanas al valor Pi, y que se requiere un criterio abierto para descifrar algunos aspectos de las pirámides de Guiza que aun no tienen una explicación lógica, racional y coherente. No trato de desacreditar a nadie, cada uno tiene sus argumentos valideros, si Usted menciona que solo usaron la Cuerda, Palmas y Dedos respeto su criterio, Si otros mencionan que alinearon los puntos cardinales de las pirámides con la estrella polar de ese tiempo, también respeto su criterio, pero como lo menciona el Blog debemos ser escépticos, Yo dudo que con tales métodos hayan logrado la precisión obtenida y tengo mi mente abierta para cualquier posibilidad de investigación científica seria y confiable que se realice sobre las pirámides, que a cada rato nos sorprenden con Nuevos Misterios.
Cordiales Saludos
CarlosR
2/12/15 16:48
@ Someone:
Tú no entiendes, detrás de los pobres egipcios, sus cuerdas y sus clavos, estaban los Annunaki con sus calculadoras biónicas.
William Clavijo Robinson
2/12/15 23:34
VERSIÓN FINAL de los cálculos utilizados por los egipcios en el Diseño Arquitectónico de la Pirámide de Keops
8 = Perímetro del cuadrado circunscrito al círculo unitario
Pi/2 = Base triángulo menor inscrito en cuadratura de círculo unitario
√ 8 = Diagonal del Cuadrado circunscrito al círculo unitario
Pi/2 + √8 = 4,39922345154109
√8 – √8/100 = 2,80014285349873
4,39922345154109 * 100 = 439,922345154109 (Base Keops en codos)
2,80014285349873 * 100 = 280,014285349873 (Altura Keops en codos)
439,922345154109 * Pi/6 = 230,3428 (Base Keops en metros, promedio de los 4 lados)
280,014285349873 * Pi/6 = 146,615137 (Altura Keops en metros)
El resultado en metros se ajusta a las mediciones de Sir. William Matthew Flinders Petrie.
Muchos Saludos
sergio rodriguez
21/09/16 01:49
las medidas que muestran de la base de la pirámide no coinciden con las que se muestran en wikipedia, a qué se debe?