Con π de pirámide
Hoy en día todavía hay mucha gente que cree que las pirámides fueron construidas por extraterrestres o atlantes. Los primeros cristianos y musulmanes creían que fue el propio Dios el que las creó. No hemos cambiado mucho en estos últimos siglos. Solo hemos remplazado una túnica por un traje espacial.
Un interesante argumento que apunta a que fue una inteligencia super avanzada la que diseñó las pirámides de la 4ª dinastía en Giza, es la presencia insolente del número [latex]\pi[/latex] en sus dimensiones, cuando según los egiptólogos, los egipcios no conocían los números reales, y solo se manejaban con fracciones de números enteros.
Recordemos que el número [latex]\pi[/latex] es el resultado de dividir el perímetro de una circunferencia entre su diámetro, y su valor es 3,1416.
¿Dónde aparece el número [latex]\pi[/latex] en las pirámides?
Los lados de la gran pirámide de Giza tienen las siguientes longitudes
- Lado Oeste: 230,357 m
- Lado Norte: 230,253 m
- Lado Este: 230,391 m
- Lado Sur: 230,454 m
Por lo tanto, el perímetro de la pirámide es:
P = 230,357 + 230,253 + 230,391 + 230,454 = 921,455 m
La altura de la pirámide es 146,5 m.
Si el perímetro de una circunferencia es:
P = 2 · [latex]\pi[/latex] · r
donde r es el radio, entonces
$latex \pi = { P \over 2 * r}$
Sustituyendo P por el perimetro de la pirámide y r por la altura obtenemos:
$latex \pi = {921,455 \over 2* 146,5} = 3,1449$
Una buena aproximación al número $latex \pi$, con un error de solo 3 milésimas. ¿Casualidad?
El papiro matemático de Rhind
Este papiro data del 1800 a.C. aproximadamente y contiene el enunciado y resolución de 87 problemas matemáticos, por lo que es un elemento valiosísimo para entender el nivel de conocimiento que tenían los egipcios en la época de las pirámides. En este papiro hay varios problemas interesantes, pero fijémonos ahora en el número 50. El enunciado del problema plantea cómo calcular el área de un círculo que tiene 9 unidades de diámetro (digamos metros). Para resolverlo se explica que hay que quitar 1/9 del diámetro y al resultado multiplicarlo por si mismo. El resultado es el mismo que el área del circulo.
Los egipcios tenían una curiosa manera de multiplicar. Por ejemplo para calcular el valor de 8 * 9, tomaban una de las dos cifras a multiplicar y hacían una tabla como la siguiente, en la que se duplicaba el valor en cada iteración
1…8 «
2…16
4…32
8…64 «
Como se quiere multiplicar por 9, tomamos los valores asociados al 8 y al 1 y los sumamos: 72 (que es 8×9)
En el problema que nos atañe, es incluso más fácil, ya que hay que tomar el valor asociado al 8: 64 $latex m^2$(8×8). El valor real de la superficie de la circunferencia es:
A = $latex \pi$ · $latex r^2$ = 63,6173 $latex m^2$
El resultado es bastante aproximado. Pero lo más inquietante es que en base a este método de cálculo se podría inferir un valor aproximado a $latex \pi$ expresado como fracción de números enteros:
a: área
d: diámetro
r: radio (2*r)=d
$latex a = (d-{d\over 9})^2$
$latex a= (d * (1- {1 \over 9}))^2$
$latex a= (d * {8 \over 9})^2$
$latex a= d^2 * {64 \over 81}$
$latex a= (2 * r)^2 * {64 \over 81}$
$latex a= 4 * r^2 * {64 \over 81}$
$latex a= r^2 * {256 \over 81}$
Según esta aproximación, los egipcios estaban aproximando a $latex \pi$ con la fracción $latex {256 \over 81}$ = 3,1605. ¿Otra coincidencia? Posiblemente si. Lo más seguro es que los egipcios empíricamente se hubiesen dado cuenta de que la aproximación detallada en el problema 50 del papiro de Rhind era lo suficientemente buena para darla por válida.
Si realmente hubiesen descubierto este factor constante en todas las circunferencias, no lo manejarían como $latex {256 \over 81}$, sino como fracciones de numerador igual a la unidad:
$latex {256 \over 81}$ = 3 + $latex {1 \over 9}$ + $latex {1 \over 27}$ + $latex {1 \over 81}$
Pero estas fracciones son muy incómodas de manejar en el sistema egipcio de multiplicación, pues todos los denominadores son impares, y ellos siempre trataban de evitarlos.
Explicaciones
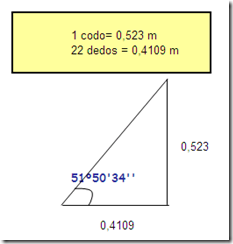
Una explicación sencilla a la presencia de $latex \pi$ en las proporciones de la gran pirámide es la manera en la que se construían. Por ejemplo, en los problemas 56 a 60 del papiro matemático de Rhind se enseña a calcular la pendiente de las paredes de una pirámide, lo que ellos conocían como seked. Para los egipcios el seked era la distancia en el plano horizontal que se desplaza la pared de la pirámide por cada codo que se levanta en altura. Un codo equivale aproximadamente a 0,523 metros. Un codo = 7 palmos y un palmo=4 dedos.
La pirámide de Keops tiene un seked de 22 dedos, o bien de 5½ palmos. Eso quiere decir que por cada codo que se eleva, pierde 5 palmos y medio en el plano horizontal.
Debido a la relación entre dedos y codo de 1 a 28, los egipcios podían construir con 28 sekeds distintos, desde 1, casi vertical, a 28 (45 grados). Todas las pirámides de Egipto están construidas con uno de estos sekeds, pero los mas comunes eran el 22, el 21, 19, 23 y 24. Hay alguna excepción que tiene un seked de más de 28 dedos, como la de Sneferu (30), con una inclinación algo menor de los 45º.
Los egipcios construían las pirámides desde fuera hacia dentro. Primero colocaban las piedras exteriores que eran cortadas con el seked de la pirámide, y luego se rellenaba el interior. Al llevar implícito este ángulo de inclinación de 51º 50’ 34”, por mera coincidencia se cumple lo expuesto en la primera parte de este artículo, al igual que ocurre en las pirámides de Huni y de Niuserra, y no ocurre por ejemplo en la de Micerinos, que tiene un seked de 23.
Hay otra teoría que a mi me gusta más (aunque no quiera decir que sea más plausible). Al medir la longitud de los lados de la pirámide normalmente habrían usado una cuerda, pero en distancias tan grandes como 230 metros, hasta las cuerdas más sólidas tienen cierta elasticidad. Es posible que en vez de utilizar una cuerda utilizasen una rueda para medir la longitud, con lo que se evitaría este problema. Imaginad una rueda cuyo diámetro sea un codo (0,523 m.) y por tanto su perímetro sea 1,643m. Para conseguir alcanzar los 230 metros de lado de la pirámide, debió de dar 140 giros completos. Si para calcular la altura se hubiesen estimado apilar tantos diámetros como el doble de giros dados por la rueda para dibujar el lado, entonces la altura sería 2 · 140 * 0,523m = 146,44m, exactamente la altura de la pirámide. En este caso también habría quedado grabada la impronta del número $latex \pi$ en las dimensiones de la pirámide, sin que los egipcios hubiesen tenido constancia de ello realmente.
Referencias:
http://www.3viajesaldia.com/el-misterio-de-pi-y-las-piramides-de-egipto/
http://www.egiptomania.com/jeroglificos/articulo/relaciones.htm
http://www.egiptologia.org/ciencia/matematicas/aritmetica_fracciones.htm

zohar
20/06/11 19:46
¡¡¡escalofriado me quedo con la (No) explicación!!!
Casette
20/06/11 19:54
Estimado Sr. Peña, sigue jugando a los magufos. Insisto: esto no son las webs de sus amiguetes. Aquí no basta decir ‘las pruebas están por todos sitios’, sino documentarlas. Aquí no basta decir que ‘en antropología se sabe perfectamente quien construyó al hombre’ sino QUÉ antropólogos, QUÉ teoría, CÓMO se construyó. Lo demás es divagar y dárselas de perdonavidas; ‘me considero protector de la raza humana, tch, tch, no quiero ver morir a nadie’
Respecto a su pataleta infantil, decirle que he disfrutado mucho. Ver a un vendehumos perder los papeles me produce hilaridad por lo típico-tópico: ‘no tengo argumentos, ergo paso al insulto y a la descalificación’. Además ha pasado usted de la categoría MAGUFO a la de simple TROLL, y me temo que no estoy por la labor de darle a usted el alpiste que desea. ‘Los de mi calaña’ pasamos de alimentar el ego de los de la suya. ‘Vuela palomita, vuela, vuela…’ (Hannibal Lecter dixit)
Con dios y por la sombra.-
Qiong
20/06/11 19:55
@ Dr. Bacterio:
Coño Bacterio… con su lista de expertos casi consigue que me atragante con un cacahuete medio egipcio…
Cib
20/06/11 19:57
Sobre el origen del hombre hay 2 vertientes dignas de encomio, una promovida por la Ciencia (antropologia y antropo. física) y otra postulada por Enron (grupo y pandilla). La primera entra en sinergia con otras disciplinas cientificas y la otra, se evade en antagonismos metafísicos y religiosos, tan sólo comprensible para Justin Bieber.
Volviendo al hilo de Pi, hay que recordar que no sólo la civi. Egipcia obtuvo el nº Pi. En 2008 la avioneta de Lucy Pringle captó un crop-circle, de Pimerísima calidad (*), su impacto en ella fué tal, que desde entonces se hace llamar Lucy PIngle. Felicidades …
(*) http://www.lucypringle.co.uk/photos/2008/uk2008af.shtml#pic6
Casette
20/06/11 20:04
A mí los únicos Pringles que me gustan son las patatas fritas. Que por otro lado llevan de todo menos patata (leer la fórmula de los susodichos snacks da bastante pánico)
Soy bastante escéptico respecto a que inteligencias de cualquier tipo (sea Gaia, intraterrenos o los hombrecillos verdes de Raticulín) no tengan otra forma de comunicarse que chafar tallos de campos de cultivo…
Manuel
20/06/11 20:05
Hola!
Enhorabuena por el blog y el activismo escéptico, tan falto hoy día.
No entiendo muy bien este artículo, que dice que los egipcios usaban pero no conocían el número Pi, mientras que en un artículo anterior (https://lamentiraestaahifuera.com/2010/03/08/los-secretos-de-las-piramides/)Adela, estudiosa de la civilización egipcia, decía: «Recordemos que los Egipcios habían ya descubierto el teorema de Pitágoras así como el número pi. Utilizaban el teorema comúnmente para establecer las lindes de los campos después de la inundación anual del Nilo.»
No me ha quedado muy claro, ¿conocían el número Pi o no?
Lampuzo
20/06/11 20:11
Rafael Peña dijo:
Entiendo tu postura…, no es cuestión que nadie muera de una «sobreexposición al conocimiento de la verdad..» Ahora bien.., si te sirve de apoyo para tu revelación, en este sitio estamos acostumbrados a manejar la verdad y estoy seguro que podríamos soportarlo…, así que cuenta.., cuenta.
Ahora bien.., si te sirve de apoyo para tu revelación, en este sitio estamos acostumbrados a manejar la verdad y estoy seguro que podríamos soportarlo…, así que cuenta.., cuenta.
Si aún así tuvieras reticencias.. siempre nos podrías dar el nombre del catedrático de Antropología de la Universidad de Sevilla ó en su defecto el de alguno de los otros contertulios, y se lo preguntamos nosotros…
En caso que ninguna de estas dos opciones sea factible.., lo lógico, por nuestra parte, sería pensar que hemos dado con un nuevo «descubridor de unicornios rosas porque yo lo valgo..» y no es así.. ¿Verdad..?
Aquí quedo a la espera..:averquepone:
Lampuzo
20/06/11 20:15
¡Don Menti…,superior… jamón 5 jotas..! 😉
Pame
20/06/11 20:44
El valor aproximado de π en las antiguas culturas se remonta a la época del escriba egipcio Ahmes en el año 1800 a. C., descrito en el papiro Rhind.
Este artículo habla de la Cuarta Dínastia. La Cuarta Dinastía Se inicia cerca de 2630 a. C. con el reinado de Seneferu y termina ca. 2500 a. C. con el de Shepseskaf (o tal vez con Dyedefptah, citado por Manetón).
También me inclino a que el número apareció al hacer rodar algo cilíndrico como un tambor para efectuar mediciones de larga distancia
lamentira
20/06/11 20:49
@ Lampuzo:
Muchas gracias.
lamentira
20/06/11 20:59
@Manuel:
Adela es la mujer de un amigo mio aficionada a la egiptología. Le envié un cuestionario y me lo respondió tan bien como pudo. Desde entonces he investigado bastante en primera persona sobre este tema y puedo decirte que los egipcios no conocían el teorema de pitágoras. Lo que si conocían era el triángulo sagrado (triangulo de lados 3,4,5) y también desconocían el número pi.
Ya edité hace unas semanas el artículo para corregir un error. Creo que voy a editarlo y coregirlo de nuevo.
lamentira
20/06/11 21:12
@ Rafael Peña:
Yo quiero morir. Dame una sobredosis de verdad aquí o por correo.
Pame
20/06/11 21:41
Los antiguos eran antiguos, pero no idiotas. Esto lo olvidan los magufos y conspiranoicos, olvidan que la inventiva humana es patrimonio de todas las culturas y de todas las épocas.
Hablando del teorema de pitágoras, una curiosidad:
Tablilla babilónica, conocida por el número de catálogo Plimpton 322
Esta tablilla data del período babilónico antiguo (ca.1900 a 1600 a.C.). Es tan sólo el fragmento de una tabla más grande, a
Seis primeras filas de la tablilla:
1,59,0,15_______________________1,59____________2,49____________1
1,56,56,58,14,50,6,15____________56,7____________1,20,25__________2
1,55,7,41,15,33,45_______________1,16,41_________1,50,49__________3
1,53,10,29,32,52,16______________3,31,49_________5,9,1____________4
1,48,54,1,40____________________1,5_____________1,37_____________5
1,47,6,41,40____________________5,19____________8,1______________6
Recordemos que los babilonios utilizaban la numeración sexagesimal, por lo que debemos convertir las cifras a nuestra numeración antes de cualquier intento.
Tomemos la sexta línea, por ejemplo:
1,47,6,41,40________5,19______8,1______6
Tras la conversión en decimal obtenemos:
1,785192901_______319________481________6
La conversión se realiza de la siguiente forma:
1,47,6,41,40=1·600+47·60-1+6·60-2+41·60-3+40·60-4=1,785192901
Y cual es la relación? la relación es la siguiente. Si tenemos un triángulo rectángulo cuya hipotenusa valga 481 y uno de sus catetos 319, entonces el otro cateto, mediante el teorema de Pitágoras vale 360.
El cociente entre la hipotenusa y este último cateto es 481/360= 1,33611111, y su cuadrado vale 1,785192901; exactamente hasta el noveno decimal la primera cifra de la primera fila de la tablilla.
Parece ser que sin conocer el teorema de Pitágoras, se conocían los valores de ciertas ternas pitagóricas: ternas de números enteros a,b,c que cumplían que a2=b2 + c2.
Javi
20/06/11 22:23
@ Pame:

HAL9000
20/06/11 22:55
Rafael Peña dijo:
En mi ultima charla con varios catedráticos de historia de Sevilla, me dijeron algo sorprendente :
Aquí en antropología se sabe perfectamente quien construyó al hombre, pero esa información está reservada por ahora … hay gente que cree que sabe y se podría morir al conocer mas sobre su pasado como especie.
Porfa, porfa, porfa… Sr. Peña… díganos quien construyó al hombre, no se haga Ud. de rogar que tiene a toda la audiencia sobre ascuas, hombre…
Saludos.
Dr. Bacterio
21/06/11 11:40
A los interesados en el tema de las matemáticas antigüedad, aquí os dejo una serie de tres documentales llamada «El legado de pitágoras» en la que se ahonda en los conocimientos matemáticos de las distintas civilizaciones antiguas y las distintas pruebas arqueológicas que tenemos de las mismas.
Podréis ver, entre otras cosas, la tablilla a la que hace referencia Pame en su excelente post o el papiro de problemas matemáticos egipcios comentado por Lamentira. Además veremos las aplicaciones que estas culturas dieron a estos conocimientos plasmadas en sus construcciones
Imprescindible. Os lo dejo para ver online:
Cap 1: http://www.megavideo.com/?d=P9QZKOAZ
Cap 2: http://www.megavideo.com/?d=XYFR6W8J
Cap 3: http://www.megavideo.com/?d=8A6W34XW
Saludos.
Tru
21/06/11 13:50
Gracias ; me acompañarán durante el café.
Dr. Bacterio
21/06/11 16:58
@Tru:
Te gustarán, ya me contarás!
NewZealander
21/06/11 18:21
Que nos digan quien construyó al hombre ya ¡¡¡Me cago en dios!!!
maria
27/03/12 02:46
yo digo las piramides con problemas con numeros enteros esque la pro de mi escuela dio algo re difisil y no lo puedo hacer nececito un ayudita
CarlosR
27/03/12 03:00
NewZealander dijo:
Nadie. Salimos de la sopa primordial hace como 4300 millones de años.
Amildao
27/03/12 05:22
La niña esta pidiendo una ayudita ché!
CarlosR
27/03/12 05:41
Amildao dijo:
Sé… un maestro, un diccionario y un libro de gramática por el amor de Alá!!!!
Anónimo
24/07/12 21:36
«Es posible que en vez de utilizar una cuerda utilizasen una rueda» … Lamentablemente los egipcios no conocían la rueda en esa época.
lamentira
25/07/12 00:20
@ Anónimo:
El que no la usasen para desplazar las piedras no quier decir que no la conociesen. Las ruedas en la arena no son una buena solución. Si tienes niños pequeños lo habrás comprobado la primera vez que intentaste meter un carrito en la playa.